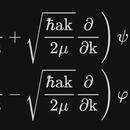
通过连续型行波法求解薛定谔方程，得到概率波的解是用从初相相同波矢不同的一系列的行波的叠加，每一列行波的波矢都对应着一个动量，其权重就是相应的概率；也可以从相空间求解，同时得到波矢相同的不同初相的一系列行波的叠加，每一列行波的初相都对应着一个位置，其权重就是该位置的概率。这样分解也反映了粒子在客观上不能同时具有确定的位置和动量。把定态的概率波（驻波）分解为一系列行波，之后对其时频分析，给出从数学与统计学角度构建不确定关系和从平均值算子与对易子构建不确定关系这两种证明方法，体现了对海森堡不确定性关系中“波”的理解。

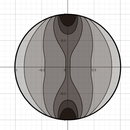
1引言 对于某一些非双折射材料，在其受到外力时自身结构会产生变化，由此而造成双折射现象。根据这一现象，我们就可以利用圆偏振光穿过形变材料，在形变材料内分为寻常光线和非寻常光线，两束光线折射率不同，由此在两束光射出形变材料时，会产生相位差。我们通过测量其干涉条纹，从而得反推及应力分布。基于这一理论。产生了光测弹性学，并在上世纪八九十年代发展成熟，至今在各方面都有着广泛的应用。

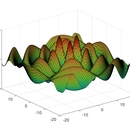
在波动光学中，对光学的各种波动现象的研究，往往涉及到计算光程的问题，这就对所采用的光学折射率数值的精确性有着很高的要求，现拟采用低频高能流密度的偏振激光，以横向磁场振动模式，使之在圆柱形谐振腔产生稳定的驻波场，建立柱谐数学模型，以亥姆霍兹方程描述，采用电磁学边界条件，构造史图姆——刘维尔本征值问题，通过对腔内特定点时变电场的测量，并对测量结果进行频谱分析，结合数学模型中对贝塞尔函数零点的计算，得出固体，液体或者气体的介电常数，从而实现对固体，液体或者气体的折射率进行精确的测量。采用这种圆柱体谐振腔内横向磁场振动模式的激光谐振法，结合数学模型，理论上，可以将气体折射率的精度达到十的负八次方量级，可以满足大多数波动光学实验对折射率精确性的要求，在优化一些波动光学实验的方面具有重大价值。此外，利用该方法的高灵敏性，还可以结合标准曲线对环境实现实时监测。